[그린경제/얼레빗 = 이규봉 교수] 인구가 늘어나고, 특히 도시에 인구가 밀집하면서 인구의 예측은 대단히 큰 사회적 관심사가 되었다. 인구의 증가 및 감소는 사회의 전 분야에 영향을 미친다. 인구가 증가할 경우 가장 큰 문제는 먹을거리일 것이다. 인구 증가에 따라서 먹을거리도 증가해야 한다. 그렇지 않다면 심각한 사회문제가 생긴다.
그뿐 아니라 아동의 증가에 따른 학교의 증설도 필요하고 향후에 그들이 독립할 때를 대비해 그들이 살 집도 증가해야 한다. 인구의 증가로 인구의 이동이 많아져 도로 건설도 필요하고 에너지 소비도 많아져 발전소 건설도 필요하다. 이러한 시설을 만들려면 자연환경의 파괴를 막을 수 없다. 그러다 인구가 줄어들면 복구가 힘들 정도로 자연을 파괴해가며 만든 기존의 많은 시설은 거의 무용지물이 될 수밖에 있다.
이미 18세기에 맬서스(T. Malthus, 1766~1834)는 이 문제를 강조하여 맬서스의 법칙을 발표했다. 이 법칙의 요지는 앞으로 인구는 급격히 증가하는 반면 먹을거리는 천천히 증가한다는 것이다. 그래서 심각한 사회문제가 발생하기 이전에 이를 막기 위해 산아제한을 해야 한다고 주장했다. 그 결과 각 나라에서는 저출산을 장려하는 가족계획을 하게 되었다. 우리나라도 예외는 아니었다. 경제개발계획에 따라 강력한 가족계획이 시행되었다.
현재 우리나라 30대 이후에서 60대 이전의 세대는 이에 따른 나라의 산아제한 정책에 따라 출생되었다. 대부분의 집에서 아들 딸 가리지 않고 둘 만 낳게 되었고 이것이 더 심해져 심지어 하나만 낳기 운동도 벌어졌다. 만일 아이를 그 이상 낳으면 차별과 피해를 감수해야 했다. 그 결과 비록 낙태가 불법이긴 하지만 사문화 되어 무분별한 낙태가 암암리에 시행되었고, 이로 인해 수많은 생명이 완성되기도 전에 사라졌다. 적절한 피임을 하지 않은 대부분의 많은 가정은 낙태의 경험을 갖게 되었다.
 |
||
이대로 가면 인구가 늘기는커녕 오히려 줄어들게 된다. 그렇게 되면 노령인구는 증가하고 젊은이들은 줄어든다. 세금은 충분히 걷히지 않아 노인을 포함한 사회복지에 심각한 영향을 줄 것이다. 남아도는 부동산으로 거의 모든 부동산은 폭락할 것이며 연금수혜자도 큰 타격을 입을 것이다.
인구의 변화와 맬서스의 법칙
시간에 따라 개체의 수는 달라지고 동일한 시간에 서로 다른 개체수가 생길 수는 없다. 이러한 현상을 수학에서는 함수라고 한다. 그러므로 시간에 따른 개체의 수는 함수가 된다. 기호를 사용하여 시간에 따른 한 개체의 수를 함수 p(t)라고 하자. 일반적으로 개체수가 많으면 출생하는 비율도 늘어난다. 개체수가 늘어나는 비율이란 앞에서 설명했듯이 개체수를 시간에 대해 미분한 것으로 dp/dt라 표현한다. 개체수가 늘어나는 비율은 현재의 개체수에 비례하므로 다음과 같은 수식이 성립한다.
dp/dt=k1p
여기서 출생률 k1은 양수이다. 처음 개체수를 p0라고 하면 이 문제의 수학적모델은 다음과 같다.(믿으면 복이 오니 이제부터 나오는 수식이 어려우면 믿고 넘어간다.)
dp/dt=k1p, p(0)=p0
사람의 경우 오직 자연사만 인정한다면 사망률 k2 역시 현재 인구에 비례한다. 사망은 인구를 감소하게 하므로 인구의 증가율은 출생률에서 사망률을 뺀
dp/dt=(k1-k2)p
이다. k=k1-k2라 하면 이 방정식은 다음과 같이 간단히 표시된다.
dp/dt=kp, p(0)=p0
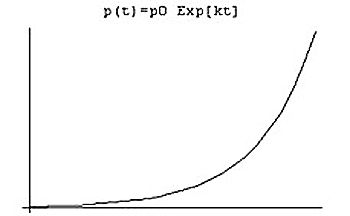
여기서 k가 음수이면 늘어나는 비율이 음수가 되어 개체수는 감소하고, 0이면 변화가 없고 그리고 양수이면 증가한다. 이 방정식의 해 p(t)=p0ekt 의 그래프는 다음과 같다.
 |
||
인구의 변화와 벨허스트의 법칙
맬서스의 법칙을 나오게 한 방정식은 너무도 많은 조건을 무시했다. 인구가 증가하는 요인은 출생 하나로 볼 수 있지만 인구가 감소하는 요인인 사망은 그 종류가 너무도 많다. 그러나 맬서스의 법칙은 인구가 감소하는 요인으로 오직 자연사만 인정했다. 이에 조건을 하나 더 추가해보자. 사람이 사회생활을 하면서 오는 경쟁관계에 의해 사망하는 경우이다. 둘 만 있다고 가정하면 둘 사이에 오는 관계는 너와 나 하나뿐이다. 셋이 있으면 셋 중 둘이 경쟁하는 관계가 세 가지가 있다. 현재의 개체수를 p라고 하면 각각의 두 개체 사이의 경쟁관계는 p(p-1)/2개 있다. 이러한 경쟁관계에 비례하여 사망하는 경우도 많아지므로 다음 조건이 감소 요인으로 추가된다.
k3p(p-1)/2
이 조건을 추가하고 a=k+k3/2 그리고 b=k3/2라고 하면, 인구의 증가를 예측하는 방정식은 다음과 같이 단순하게 표현할 수 있다.
dp/dt=p(a-bp), p(0)=p0
이 방정식을 벨허스트 모델이라 하며 이 방정식을 만족하는 해는 다음과 같다.
p(t)=ap0/{bp0+(a-bp0)e-at}
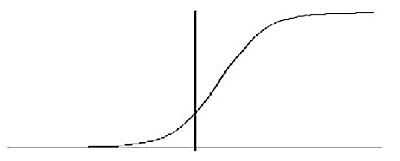
이다. 이 해를 로지스틱 함수라 한다. 이 함수의 분모에서 a는 양수이므로 시간 t가 점점 커질수록 e-at 가 매우 빠른 속도로 작아져 (a-bp0)e-at는 0으로 가까이 간다. 그러므로 p(t)는 a/b에 가까이 간다. 따라서 개체수는 a/b를 넘을 수 없다. 이 수를 균형개체수라 한다. 다음 그림은 a/b가 초기의 수보다 클 때 개체수의 변화를 보여준다.
 |
||
다음 편에서 벨허스트 모델의 해인 로지스틱 함수의 그래프가 2012년 대선의 그래프와 비슷하여 부정선거 시비가 나온 점에 대해 알아본다.

