[그린경제/얼레빗 = 이규봉 교수] 컴퓨터가 매우 실용화되면서 종이의 소비가 줄어들 것으로 기대했다. 그러나 화면 속의 글씨보다는 종이 위에 인쇄된 글씨가 보기 편해 출력을 또 하기도 한다. 중요한 자료의 보관을 위해서는 디지털 저장 뿐 아니라 고전적인 인쇄물로 저장하는 습관도 아직 갖고 있다. 특히 컴퓨터의 인쇄술 발전은 홍보물을 값 싸게 남발하여 종이의 소비를 크게 줄이지는 못했다. 종이를 소비하는 것은 나무를 벌목하는 것이나 다름없어 이는 환경에 매우 나쁜 영향을 끼친다.

▲ 복사용지들
미국을 제외한 대부분의 나라에서는 같은 규격의 컴퓨터 용지를 사용한다. A와 B로 시작하는 종이가 그것이다. 이 종이에는 일정한 특징이 있다. 그것은 비록 크기가 다를지라도 모양이 같다는 것이다. 모양이 같다는 것은 닮은꼴로 적당한 비율로 축소하고 확대하면 서로 다른 규격의 종이로 출력할 수 있다. 따라서 닮은꼴은 종이의 낭비를 막아줄 수 있다. 여기에 숨어 있는 수가 있으니 바로 2의 제곱근인 √2이다. 이 수의 크기는 밑변과 높이가 1인 직각삼각형의 빗변의 길이와 같다.
복사용지에 숨겨진 수
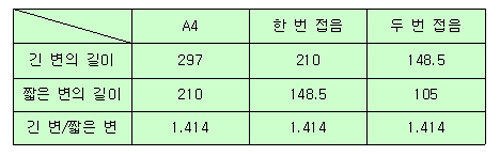
우리가 주로 사용하는 복사용지는 A4나 B4 또는 B5를 많이 사용한다. 그중 가장 많이 사용하는 A4의 긴 변의 길이와 짧은 변의 길이를 재고, 다시 긴 변의 중간을 중심으로 반으로 접은 후 나온 사각형의 긴 변의 길이와 짧은 변의 길이를 재면 다음 표와 같다.
 |
||
한편 복사용지가 아닌 일반용지의 길이를 복사용지와 같은 방법으로 재었더니 아래 표와 같았다.
 |
||
복사용지에서 긴 변의 길이 대 짧은 변의 길이의 비는 항상 1.414이다. 이 수는 √2에 매우 가까운 수이다. 종이의 가로 대 세로의 비가 √2가 되면 반으로 접어도 그 모양이 변하지 않아 확대와 축소를 통해 서로 다른 규격의 종이로 변환을 자유롭게 한다. 따라서 √2라는 수는 규격이 서로 달라 잘못 잘라져 나가는 종이의 낭비가 없도록 하는 아주 환경적인 수다.
닮은꼴을 유지하는 2의 제곱근
한 직사각형의 긴 변을 반으로 접어도 원래의 직사각형과 모양이 같다고 하자. 편의상 이 직사각형의 한 변의 길이를 1이라 하고 다른 한 변의 길이를 x라 하자(여기서 1<x<2). 그러면 긴 변을 반으로 접은 직사각형의 긴 변의 길이 대 짧은 변의 길이의 비는 1:x/2이다. 원래의 직사각형과 같은 모양이라는 뜻은 닮은꼴로 두 비가 서로 같다는 것이다. 따라서
1:x/2 = x:1
이 성립한다. 등호를 중심으로 안쪽 항과 바깥쪽 항의 곱은 같으므로 x2=2을 만족한다. 따라서 x=√2가 된다. 즉 직사각형의 긴 부분을 반으로 접어도 원래의 직사각형과 모양과 똑같으려면 직사각형의 두 변의 길이의 비가 √2가 되어야 한다는 뜻이다.
한편 어떠한 일반용지도 두 번 반복해서 접으면 가로와 세로의 크기가 모두 반으로 되어 두 번 접힌 용지는 항상 원래 용지와 닮은꼴이다. 그러나 가로와 세로의 비가 √2가 아니면 한 번 접힌 경우는 원래의 용지와 다르다.
복사용지의 제작
우리가 가장 자주 사용하는 복사용지는 A4이다. 실측을 통해 알아본 것처럼 이 A4 용지의 규격은 210mm×297mm이다. 긴 변의 길이 대 짧은 변의 길이의 비는
297/210 ≈ 1.414286
로 √2와 거의 같다. 즉 A4 용지는 반으로 접으면 원래의 모양과 같게 나오도록 제작된 것이다.
종이는 공장에서 전지라고 부르는 큰 규격의 종이를 절반으로 자르고, 이를 또 다시 절반으로 자르는 과정을 반복하여 만들어진다. 전지를 반으로 자른 것이 반절지, 가로 세로로 각각 이등분하여 나온 종이를 4절지라 하며, 4절지를 반으로 자른 것을 8절지, 8절지를 반으로 자른 것을 16절지라 한다. 즉, n절지는 전지를 똑같은 크기로 n등분한 종이다.

독일공업규격위원회(Deutsche Industrie Normen)에서는 큰 종이를 잘라 작은 종이를 만드는 과정에서 종이의 낭비를 최소로 줄일 수 있도록 인쇄, 컴퓨터, 편지, 책 등에 이용되는 종이의 형태와 크기를 선택했다. 적절한 규격을 선택했을 때, 예를 들어 컴퓨터 용지의 절반을 편지지로 하고 편지지의 절반을 메모지로 메모지의 절반을 또 다른 용도로 사용한다면 종이를 많이 절약할 수 있을 것이다. 앞서 설명했듯이 종이를 절반씩 나누어 가는 과정에서 그 모양이 변하지 않게 하려면 종이의 가로대 세로의 비는 √2가 되어야 한다.
B 용지는 A 용지보다 1.5배 넓다
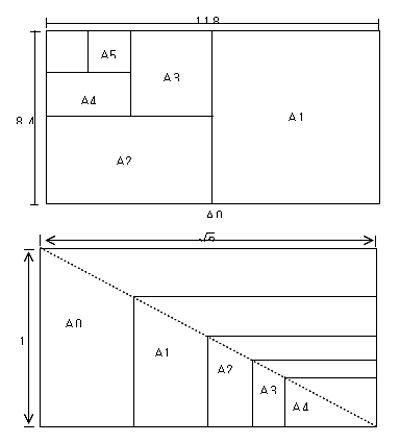
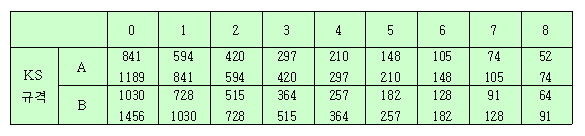
전지인 A0 용지의 두 변의 길이는 각각 1189mm와 841mm로 그 비는 약 1.4138이며 넓이는 1189×841=999949mm2 으로 약 1m2이다. 즉, A0 용지는 넓이가 1m2이고 가로 대 세로의 비가 √2가 되도록 만든 종이이다. 이 종이를 절반으로 자른 종이를 A1, 다시 A1을 절반으로 자른 종이를 A2라 한다. 같은 방법으로 A3, A4, A5를 만든다. 즉, A4는 A0를 네 번 반복하여 절반으로 자른 종이로 A0 용지를 16(=24)등분한 16절지이다. A 용지를 다음 그림 과 같이 모두 포개놓으면 그 닮은 모양을 알 수 있다.
다음 표는 ISO 종이 규격이며 동시에 KS 규격이다. ISO 종이 규격은 유럽지역에서 가장 공통적으로 쓰이고 있는 표준 규격이며 미국은 A4 대신에 주로 레터(letter)지를 사용하며 레터지의 규격은 216×279mm(8.5'×11')이다. 물론 레터지는 반으로 접으면 같은 모양이 나오지 않는다.
 |
||

