[한국문화신문 = 이규봉 기자]  순정율은 작은 정수에 의한 비가 화음을 이루는 것에 기초해 프톨레마이오스가 피타고라스 음계의 진동수에서 분모와 분자가 두 자리 이상인 경우 약분이 가능한 가까운 수로 다음과 같이 대체했다. 

81/64≒80/64=5/4, 27/16≒25/15=5/3, 243/128≒240/128=15/8 

따라서 C의 주파수를 1로 했을 때 피타고라스 음계와 순정율의 진동수의 비는 다음 표와 같다.

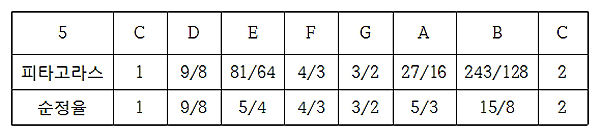
순정율에서는 ‘도미솔’, ‘솔시레’, ‘파라도’ 화음은 모두 진동수 비가 4:5:6이 된다. G7화음인 ‘솔시레파’의 진동수의 비는 36:45:54:64이나 64를 63으로 바꾸면 이는 4:5:6:7로 간단히 표현이 된다. 보통 사람은 G7화음을 36:45:54:64로 듣기보다는 4:5:6:7의 단순한 정수비로 듣게 된다고 오일러는 주장한다.  

순정율에서 C장조의 노래 ‘도도솔솔 라라솔’을 한 음 올려 조옮김하면 D장조 ‘레레라라 시시라’가 된다. 이때 원곡의 ‘도-솔’의 진동수 비는 2:3이나 조옮김한 곡의 ‘레-라’는 27:40으로 서로 다르다. 이 차이는 불협화음으로 인식할 정도로 크다. 이처럼 순정율도 조옮김이 불편하기는 피타고라스 방법과 마찬가지이다. 이를 극복한 것이 평균율이다. 

앞서 본 것처럼 피타고라스 음계나 순정율은 이웃한 음 사이의 음정의 비가 균등하지 않다. 평균율은 옥타브 사이에 있는 12개 음의 비를 균등하게 나눈 것이다. 진동수가 1인 음과 2인 옥타브 음 사이에 12개 음을 똑같이 나누려면 그 간격을 12번 곱해서 2가 되어야 한다. 즉 간격을 x라고 하면 x12=2를 만족해야 한다. 따라서 평균율은 각 이웃한 음정의 비를 인위적으로 12번 곱해서 2가 되게 만든 방법으로 이 비는 유리수가 아닌 무리수이다. 이로서 조옮김이 자유로워져 서양음악에서는 화성이 발달한다. 피타고라스 방법과 순정율은 유리수에 기반을 둔 반면 평균율은 무리수에 기반을 두었다.  

음 간격을 보다 정밀하게 분석하기 위해 한 옥타브를 12이 아닌 1200칸으로 균등하게 나누어 그 한 칸을 ‘센트(cent)’라고 한다. 따라서 반음의 간격은 100센트이고 온음의 차이는 200센트가 된다. 그러면 사람이 구별할 수 있는 최소의 음정은 6센트 정도이며 피타고라스 콤마는 약 24센트가 된다. 기준음의 진동수를 1로 보았을 때 어떤 음의 진동수가 f이면 그 음의 센트는 1200x log(f)로 계산 할 수 있다. 여기서 log의 밑수는 2이다. 다음 표는 피타고라스 음계, 순정률, 평균율 그리고 삼분손익법에 의한 음계를 센트로 비교한 것이다.

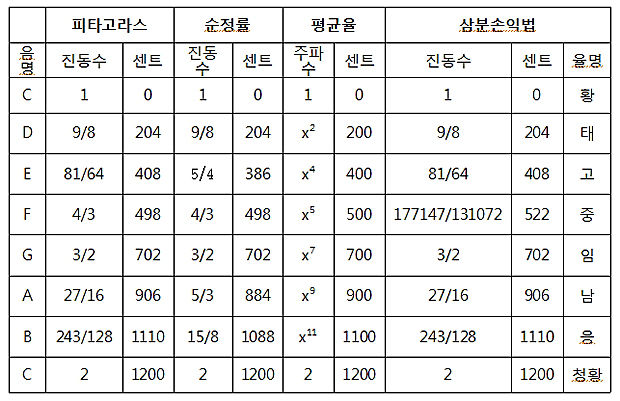
▲ <여기서 x는 12번 곱해서 2가 되는 수>

연재를 마치며 

모두 28번에 걸쳐 칼럼을 기고했다. 전공으로서 수학을 제외하고 필자의 관심 분야는 참으로 다양했다. 언제부터인지 기억이 나진 않지만 수업 시간에 특히 미분방정식 시간에 수학의 결과가 내 관심 분야에서 나의 주장을 펴는 데 큰 도움이 된다는 것을 알게 되었다. 해마다 반복해 강의하면서 그 범위가 넓어져 갔고 강의시간에 자연스럽게 수학의 결과를 갖고 수학과 전혀 다른 분야를 설명했다. 수업 뒤에 그 내용을 다시 기억해 내어 기록한 세월이 10여 년 흐른 후 책 《수학의 창을 통해 보다》를 낼 수 있었다. 

▲ 수학은 폭 넓은 사고로 삶의 질을 높여주는 학문이다.(그림 이무성 한국화가)

나는 이것을 <스토리텔링 수학>에 견주어 <수학으로 이야기하기>라고 한다. 전자는 수학을 이야기로 풀어 수학을 이해하기 쉽게 교육하는 것이고, 후자는 수학을 잘 아는 사람이 자신의 관심 분야에 대한 주장을 수학의 결과를 이용해 설명하여 일반인에게 수학의 유용성을 알리는 것이다. 수학을 공부하는 것은 결코 헛된 것이 아니다. 수학이 발전하지 않았다면 우리는 현재와 같은 문명을 누릴 수 없었을 것이다. 수학의 결과를 이용해 자신들의 주장을 펴는 글을 자주 쓴다면 수학은 보다 쉽게 대중화될 것이다.  

수학은 당신을 괴롭히는 학문이 아니라 폭 넓은 사고로 삶의 질을 높여주는 학문이다. 

(*) 《수학과 교육》 2015년 109호에 실린 내용을 재구성하였다.