[그린경제/얼레빗=이규봉 교수] 러시아의 수학자 로바체프스키는 1829년 비유클리드 기하학에 관한 최초의 논문 <기하학의 원리에 관하여>를 러시아어로, 1840년 <평행선 이론에 대한 기하학적 연구>를 독일어로 발표하였다. 여기서 그는 평행선의 존재를 하나 이상으로 가정하였다.
헝가리의 볼리야이도 로바체프스키와는 독립적으로 1832년 “만일 한 점을 지나 주어진 직선과 평행인 직선이 하나 이상 있다”라는 가정 하에 모순이 없는 새로운 기하학을 발표했다. 이 논문은 엄청난 비판을 받았을 뿐 아니라 이미 3년 전에 로바체프스키가 러시아 잡지에 발표했음을 알고 볼리야이는 정신적 우울증에 빠져 더 이상 연구를 발표하지 않았다. 독일의 가우스도 독립적으로 볼리야이가 의문을 제기하기 전에 이미 새로운 기하학을 알고 있었다. 그러나 그는 전혀 연구 결과를 발표하지 않았고 그의 사후에 알려지게 되었다.
삼각형의 내각의 합은 180도보다 작다
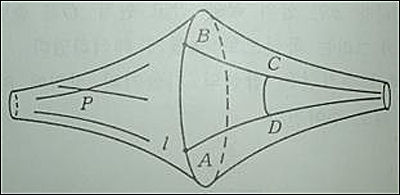
유클리드 기하학의 평행공준 대신 “한 점을 지나고 주어진 직선에 평행한 직선은 두 개 이상 존재한다.”라는 가정아래 생성된 기하학을 로바체프스키 기하학이라 한다. 이 기하학이 성립하는 모형으로 공의 안쪽이나 나팔의 겉 표면을 들 수 있다. 아래 그림에서 직선 BC와 AD는 평행선이며 직선 l에 평행하고 점 P를 지나는 직선은 적어도 두 개 이상 존재한다. 이 위에서 삼각형을 그리면 내각의 합은 180도보다 작게 된다. 즉 아래 그림에서 보듯이 오목한 면에서 삼각형을 그리면 내각의 합은 180도보다 작게 된다.
로바체프스키 기하학에서는 다음과 같은 사실이 성립한다.
(1) 임의의 직선과 그 직선 위에 있지 않은 임의의 점에 대하여 그 점을 지나고 그 직선과 평행인 직선은 적어도 두 개 존재한다.
(2) 삼각형의 내각의 합은 180도보다 작다.
(3) 모든 블록 사각형의 내각의 합은 360도보다 작다.
(4) 두 삼각형이 닮은꼴이면 그들은 합동이다.
따라서 로바체프스키 기하학에서는 두 삼각형이 닮은꼴이면 그들은 합동이므로 삼각형을 찌그러뜨리지 않고 확대, 축소시키는 것이 불가능하다. 왜냐하면 확대와 축소는 닮은꼴이므로 그것은 사진의 실물크기와 같아야만 가능하기 때문이다.
삼각형의 내각의 합은 180도보다 크다.
독일의 리만은 1854년 괴팅겐 대학의 강사 취임 강연에서 ‘기하학의 기초를 이루는 가정에 대하여’라는 제목으로 새로운 기하학을 발표하였다. 리만은 “한 평면 위에 있는 임의의 두 직선은 반드시 만난다”로 가정하여 평행공준의 평행선의 존재를 부정하였다. 유클리드 기하학의 공준 2 ‘유한직선은 무한정 연장할 수 있다’에 대하여 ‘직선의 크기가 무한하다는 것이 아니라 단지 끝이 없다거나 또는 경계가 없다.’로 생각하여 공준 1과 공준 2 그리고 평행공준을 아래와 같이 수정하였다.
(1) 임의의 두 점은 적어도 하나의 직선을 결정한다.
(2) 직선은 경계가 없다.
(5) 한 평면 위에 있는 임의의 두 직선은 반드시 만난다.
이와 같이 수정된 가정과 함께 태어난 새로운 기하학을 리만기하학이라 한다. 이 기하학이 성립하는 모형으로 아래 그림과 같이 구면을 평면으로 보았다. 이 평면에서는 직선은 표면 위의 두 점을 지나는 가장 큰 원으로 보았다. 따라서 구면에서는 직선은 경계가 없지만 유한하므로 유클리드의 두 번째 공리가 성립하지 않는다. 또한 중심에 관한 대칭점을 지나는 직선은 무수히 많을 뿐 아니라 모든 직선은 만나므로 평행선은 없다.
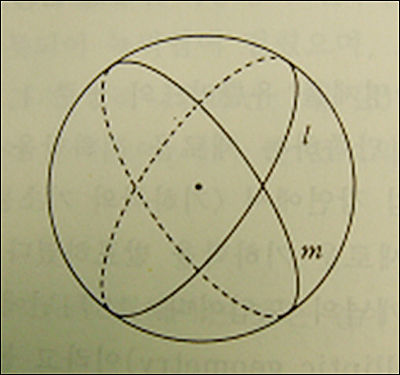
(1) 임의의 직선과 그 직선 위에 있지 않은 임의의 점에 대해 그 점을 지나고 그 직선과 평행인 직선은 없다.
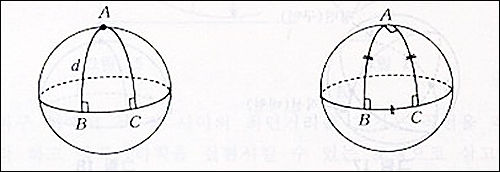
(2) 삼각형의 내각의 합은 180도보다 크다.
(3) 사각형의 내각의 합은 360도보다 크다.
(4) 두 삼각형이 닮은꼴이면 그들은 합동이다.
상대적 진리와 삼가재상
이처럼 수학의 진리는 절대적인 진리가 아니라 상대적인 진리이다. 하물며 세상살이인들 절대적으로 옳은 것은 없다. 똑같이 벌어진 일을 계집종 예쁜이가 자기 위주로 설명하니까 예쁜이가 옳다고 생각되고, 곱단이 역시 자기 위주로 설명하니까 곱단이가 옳은 것처럼 생각된다. 마찬가지로 황희 정승의 부인 말도 옳은 것이다.
아래 그림을 보자. 무슨 그림인가? 똑같은 그림을 보았는데도 보는 사람의 생각에 따라 어떤 사람은 귀부인이라 하고 다른 사람은 마녀라 한다. 누가 옳은가? 의견이 다르다고 한쪽이 틀렸다고 할 수 있는가?
배경 또는 가정에 따라 평행선이 없을 수도, 하나뿐일 수도 또는 많을 수도 있다. 삼각형의 내각의 합이 180도라는 것은 옳다. 그러나 그것만이 옳은 것은 아니다. 작을 수도 클 수도 있다. 배경을 무시하고 자신의 주장만 하면 끊임없는 논쟁이 되고 해결은 나지 않고 다툼만 커진다. 우긴다고 될 일은 아니다.
종교도 상대적으로 볼 수 있으면 평화롭게 공존할 수 있다. 하느님과 예수에 근거한 종교는 기독교, 부처님과 석가모니에 근거한 종교는 불교 그리고 알라와 마호멧에 근거한 종교는 이슬람교로 인정하는 것이다. 자신의 종교의 기준으로 다른 종교를 판단하지 말아야 한다.

황희 정승은 세 사람을 천천히 둘러보며 다음과 같이 말했다.
사람은 제 잘못은 생각하지 않고, 제가 잘한 일만을 쳐드는 법이다. 각자 잘한 일만 나에게 고해바치니, 나도 모두 다 잘했다고 할 수밖에 다른 수가 있는가?
이와 같이 무슨 일에나 긍정적으로 생각하고 남에게 자신의 주관적 의견을 내보이지 않을 때 삼가재상(三可宰相)이라 한다. 폭넓게 알면 그만큼 보이는 것이 많고 판단을 바르게 할 수 있다. 항상 상대방의 입장에서 생각하면 자존심도 상하지 않고 다툼이 없이 잘 해결할 수 있다. 수학의 모든 결과가 상대적인 진리라는 것을 알고 항상 남의 처지에서 한 번 더 생각하는 역지사지의 마음을 가질 때 우리는 다툼이 없이 평화롭게 살 수 있다.
(*)《수학과 교육》2014년 104호에 실린 내용을 재구성하였다.

