[그린경제/얼레빗=이규봉 교수] 지금은 입적하신 법정스님께선 생전에 많은 책을 저술해 많은 중생에게 따뜻한 감정을 불어놓으셨다. 스님의 책을 대표하는 것이 <무소유>다. 1976년에 초판이 나와 지금까지 가장 많이 읽힌 책이다. 필자도 대학생 시절 처음 이 책을 접했고 지금도 간간히 꺼내 보곤 한다. 이 책에서 스님이 길을 떠나는데 갑자기 집에서 기르던 난초를 아침에 양지바른 곳에 잠깐 내 놓은 것이 생각나 되돌아 왔다고 한다. 난초는 오랫동안 햇빛을 받으면 죽을 수도 있기 때문이다. 그리고는 깨달은바 난초를 남에게 주었다고 하며 다음과 같이 말한다.

▲ ≪무소유≫, 법정, 범우사
우리들이 필요에 의해서 물건을 갖게 되지만, 때로는 그 물건 때문에 적잖이 마음이 쓰이게 된다. 그러니까 무엇을 갖는다는 것은 다른 한편 무엇인가에 얽매인다는 뜻이다. 필요에 따라 가졌던 것이 도리어 우리를 부자유하게 얽어맨다고 할 때 주객이 전도되어 우리는 가짐을 당하게 된다. 그러므로 많이 갖고 있다는 것은 흔히 자랑거리로 되어 있지만, 그만큼 많이 얽혀 있다는 측면도 동시에 지니고 있다. - 법정, ≪무소유≫, 범우사, 2010, 22쪽
필요 이상으로 많이 가지면 오히려 불편을 초래한다는 스님의 말씀이다. 대표적인 것이 재물이 아닐까 한다. 살아가는데 있어서 재물은 당연히 필요하다. 그러나 그렇게 많이 필요한 것은 아니다. 하지만 많은 사람은 재물을 가능한 많이 갖고 쌓아두고 후손에게까지 물려주려고 한다. 오직하면 새해 인사로 ‘부자 되세요’ 하는 말이 나왔겠는가? 분명 여기서 ‘부자’란 재물을 뜻함이지 마음을 뜻하는 것은 아닐 것이다. 필요해서 재물을 갖게 되지만 너무 많은 재물을 쌓아두면 재물에 오히려 노예가 되어 인성을 잃어버릴 수가 있다. 현재 많이 사용하고 있는 스마트폰도 그렇다. 너무 편리해서 스마트폰을 갖지만 잠시도 그것 없이는 살 수 없을 정도가 되면 이는 중독된 것이다. 스마트폰의 노예가 되어 버린 것이다. 이러한 것을 주객전도라 한다.
공집합은 아무것도 갖고 있지 않다
법정스님이 수학의 한 분야인 집합에 대해 자세히 알고 있지는 않았을 것이다. 그러나 스님의 말씀은 이미 18세기 칸토어에 의해 새로 발견된 집합의 한 명제로 소개되어있다. 집합이라 하면 명확한 대상들의 모임을 말한다. ‘사람들의 모임’ 역시 집합이 될 수 있다. 여기서 명확함이란 참과 거짓이 분명한 것을 말한다. ‘사람들의 모임’은 사람과 사람이 아닌 것이 명확하므로 집합이 될 수 있다. 그러나 ‘키 큰 사람들의 모임’ 하면 집합이 될 수 없다. 키가 크다는 의미가 정확하지 않기 때문이다.
서울에 주민등록을 갖고 있는 사람을 서울 시민, 대전에 주민등록을 갖고 있는 사람을 대전 시민이라고 하듯이 집합에 속한 대상을 그 집합의 원소라고 한다. 즉 우리는 사람이므로 우리 각자는 ‘사람들의 모임’에 속한 원소가 된다.
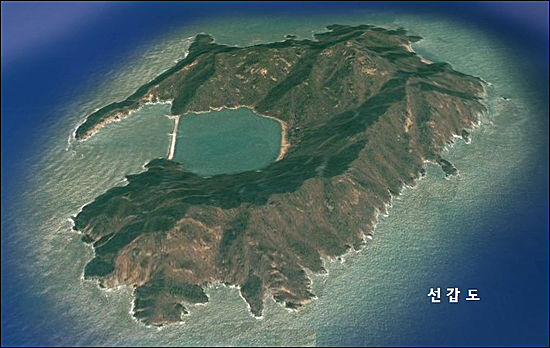
우리나라에는 무인도가 많다. 무인도는 말 그대로 사람이 살지 않는 섬이다. 우리나라에서 가장 큰 무인도는 인천의 덕적도에서 남서쪽으로 100km 떨어진 선갑도라고 한다. 그렇다면 ‘선갑도에 살고 있는 사람들의 모임’은 집합이 될 수 있는가? 물론 집합이 될 수 있다. 명제가 명확하기 때문이다. 그렇다면 집합 ‘선갑도에 살고 있는 사람들의 모임’의 원소는 무엇인가? 아무도 살고 있지 않으니 원소는 없다. 이처럼 아무 원소도 갖고 있지 않은 집합을 공집합이라고 한다. 수학에서는 공집합을 기호로 ∅라고 나타낸다.
 |
||
| ▲ 우리나라에사 가장 큰 무인도 <선갑도> ⓒ 선갑도 블로그 | ||
공집합이 수학의 무소유다
바로 이 공집합이 법정스님이 말하는 무소유 그 자체이다. 아무것도 갖고 있지 않은 공집합은 무척 자유롭고 어디에든 포함되어 있고 누구도 배척하지 않는다. 있어도 있는 둥 마는 둥이며 일체 간섭도 하지 않고 영향을 미치지 않는다. 하지만 상황이 바뀌면 모두를 없애 버릴 수 있는 막강한 힘이 있다.
한 집합 A가 다른 집합 B에 포함된다는 것은 “A에 있는 모든 원소가 모두 B에 있다”는 뜻이거나 또는 “B에 없는 원소는 A에도 없다”는 뜻이다. 이 경우 기호로 A⊂B로 나타내며 A는 B의 부분집합이라고 한다. 따라서 ‘여자들의 모임’은 ‘사람들의 모임’에 포함된다. 왜냐하면 여자는 사람이기 때문이다. 또는 사람이 아니라면 여자도 아니기 때문이다. 둘 중 어느 것도 참이므로
‘여자들의 모임’ ⊂ ‘사람들의 모임’
이 성립한다.
임의의 집합 X가 있다고 하자. 만일 어떤 것이 X에 없다고 하면 그 어떤 것은 공집합에 있을까? 당연히 없다. 왜냐하면 공집합은 어떠한 원소도 갖고 있지 않기 때문이다. 다시 말하면 ‘X에 없으면 ∅에도 없다’가 성립한다. 그러므로 공집합은 X에 포함됨을 알 수 있다. 즉 모든 집합 X에 대하여
∅⊂X
가 된다. 공집합 ∅는 가진 것이 하나도 없기 때문에 모든 곳에 다 포함된다. 즉 자신을 비우면 모든 것에 다 들어갈 수 있고 그 어떤 것도 공집합을 배척하지 않는다는 뜻이다.
없는듯한 공집합은 힘이 세다

▲ 필자가 만든 수학의 무소유 그릇
또한 공집합 ∅는 가진 것이 하나도 없기 때문에 어떤 것과 합해도 그것을 변화시키지 않는다. 있는 둥 마는 둥이다. 이것을 기호로 나타내면 다음과 같다. 어떠한 모임 X에 대해서
X⋃∅=X
이다. 그러나 아무 것도 없는 공집합에서 조차 무엇인가를 취하려고 한다면 공집합은 그것을 자기처럼 만들어 버린다. 즉 그가 갖고 있는 모든 것을 없애버린다. 이것을 기호로 나타내면 다음과 같다. 어떠한 모임 X에 대해서
X⋂∅=∅
이다. 이처럼 아무 것도 갖고 있지 않은 공집합은 어디에든 포함되어 있고 아무도 해치지 않지만 모든 것을 한 번에 날려버리는 매우 큰 힘도 갖고 있다. 이는 아무 것도 갖고 있는 것이 없기 때문에 가능한 것이다. 바로 법정스님이 말한 그 무소유를 대표한다.

