[한국문화신문 = 이규봉 교수] 인류가 생긴 이래로 나약한 존재인 인간은 자연의 위대함을 알면서 신에 의지하게 됐다. 강력한 자연에 두려움을 갖고 있는 인간은 인간의 능력을 훨씬 뛰어 넘으면서 만물을 지배할 수 있는 그 무언가가 필요했다. 그래서 인간은 신을 찾았고 만들었다. 인간이 처한 자연 환경에 따라 다양한 신들이 존재했다. 기성종교가 생기기 전에는 태양이라든가 동물 또는 자연의 형태를 숭상했다.
성경에 의하면 “태초에 말씀이 있었다.”고 한다. 구약성서에 근본을 둔 유대교가 생기면서 신은 오직 한 분이 되었다. 다양한 신을 믿던 사람들에게 오직 신은 하나뿐이라는 유일신 사상이 나타났다. 이것을 이어 받은 종교가 기독교와 이슬람교이다. “태초에 말씀이 있었다.”는 사실 여부를 떠나서 무조건 이 말을 믿는 것처럼 인간은 오직 믿음으로서 신을 대할 뿐이다. 신은 존재 하지만 볼 수도 만질 수도 따질 수도 없기 때문이다.
어떠한 종교를 믿든 공통적인 점은 인간은 유한하고 신은 무한하다는 것이다. 유한한 인간은 자신들의 방법으로 신을 대하려 한다. 유한한 인간은 절대 살아서 신을 만날 수 없다. 바벨탑을 쌓아 신에게 가까이 가려 했지만 소용이 없었다. 인간은 유한한 존재, 신은 무한한 존재. 아무리 발버둥 쳐도 인간은 신에게 가까이 갈 수는 있을지언정 절대 만날 수는 없다. 단지 마음으로 느낄 뿐이다.
인간은 유한하고 신은 영원하다. 그러므로 인간들이 사는 세상을 유한한 세상이라 하고 신들이 사는 세상을 무한한 세상이라고 해도 큰 무리가 없다. 수학도 유한과 무한을 다룬다. 일상생활에서 사용되는 셈은 모두 유한한 것으로 볼 수 있다. 그러나 무한히 많은 것은 유한한 것과 그 성질이 다르다. 유한한 것을 인간의 세상으로 본다면 무한한 것은 신의 세상으로 봐도 큰 무리가 없다.
부분과 전체의 수가 같다?
당근이 10개 있고 말이 10마리 있다고 하자. 이 둘은 서로 다르지만 수학적으로 같은 것이 있다. 그것은 각각의 개수가 서로 같다는 것이다. 당근의 수도 10, 말의 수도 10이다. 말 하나에 당근 하나씩 주면 남는 것 없이 모든 말에게 먹일 수 있다. 이러한 경우 그 둘의 개수는 같다고 한다. 하지만 말이 15 마리이면 5마리가 먹지 못한다. 이러한 경우 당근의 수가 말의 수보다 작다고 하거나 또는 말의 수가 당근의 수보다 크다고 한다.
곧 각각의 수가 유한개인 경우 하나씩 짝 지어서 서로 남는 것이 없이 딱 떨어지면 두 수는 같다고 하고, 한 쪽이 남으면 남은 쪽의 수가 다른 쪽의 수보다 더 크다고 한다. 이와 같이 두 집합 간에 하나에 하나씩 모두 짝 지울 수 있으면 두 집합은 일대일대응이라 하고, 일대일 대응이 되는 두 집합은 원소의 개수가 서로 같다고 한다.
유한의 세계에서는 전체가 아닌 그 부분은 항상 전체보다 그 수가 작다. 예를 들면, 남녀가 섞여 있는 학급에서 남학생만 모으면 항상 그 수는 학급 전체 학생 수보다 작다. 그러므로 유한의 세계에서는 전체가 아닌 그 부분을 전체에 일대일 대응 시킬 수 없다. 그러나 무한히 많은 세계에서는 이러한 일이 일어나지 않을 수 있다. 수학자 칸토어는 무한을 아래와 같이 정의했다.
전체가 아닌 그 부분을 전체에 일대일 대응 시킬 수 있으면 무한이라 한다.
우리는 자연수가 무한히 많다고 한다. 왜냐하면 자연수가 유한하다면 가장 큰 수가 있을 것이다. 그러나 그 가장 큰 수에 1을 더하면 더 커지니 가장 큰 수라는 것에 모순이 따른다. 즉 아무리 큰 자연수를 택해도 그보다 더 큰 자연수가 항상 존재하니 자연수는 무한할 수밖에 없다. 자연수가 무한하다면 칸토어가 정의한 것처럼 자연수 전체가 아니면서 그 수가 자연수 전체의 수와 같은 자연수의 부분이 존재해야 한다. 그런 것은 얼마든지 있다.
예를 들자. 자연수 전체를 N이라 하고 짝수 전체를 E라고 하자. 분명 짝수는 자연수 전체가 아닌 자연수의 부분이다. 그러나 자연수와 짝수 사이에는 일대일 대응을 맺을 수 있다. 어떤 자연수를 택해도 그것을 두 배하면 짝수가 된다. 어떤 짝수를 택해도 그것을 반으로 나누면 자연수가 된다. 그러므로 자연수와 짝수 사이에는 일대일 대응이 존재한다.
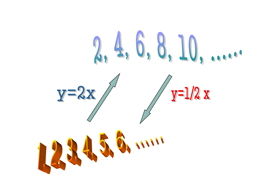
따라서 짝수는 자연수와 같지 않은 부분이지만 자연수 전체와 일대일 대응이 된다. 그러므로 자연수는 무한이다. 자연수가 무한이므로 자연수와 일대일 대응을 하는 짝수 역시 무한이다. 그러면 자연수의 개수와 짝수의 개수는 누가 더 큰가? 이 물음에 답하기 위해 이제 수학의 용어이면서 친숙한 집합이라는 단어를 사용하자.
집합은 확실한 대상의 모임이라 할 수 있다. 두 집합의 원소의 개수가 같다는 것은 두 집합 사이에 일대일 대응이 있을 때라고 했다. 모든 자연수 n에 대해 하나의 짝수 2n이 존재하고, 모든 짝수 n에 대하여 n/2을 대응시킬 수 있으므로 자연수와 짝수 간에는 일대일 대응이 된다. 그러므로 두 집합의 개수는 서로 같다. 따라서 짝수는 분명 자연수 전체가 아니면서 자연수에 포함되지만 그 개수는 서로 같다. 마찬가지로 홀수의 개수도 자연수와 같다.
이와 같은 일은 유한의 세계에서는 결코 일어날 수 없다. 유한의 세계에서는 전체가 아닌 부분은 반드시 전체보다 작기 때문이다. 그러나 무한의 세계에서는 유한의 세계에서 일어날 수 없는 일이 일어난다. 즉 전체가 아닌 부분이 반드시 전체보다 작다고 할 수는 없다는 것이다. 같을 수도 있다는 것이다.
로마의 황제이자 철학자였던 마르쿠스 아우렐리우스는 “무한은, 그 속으로 모든 것이 사라져 가는, 알 수 없는 심연이다.”라 하였고, 레오나르도 다빈치는 “자기 자신을 드러내지 않으며, 만일 자기 자신을 드러낸다면 동시에 존재하지 않게 될 그것은 무엇인가? 그것은 무한이다.”라고 하였다. “어떤 것이 무한하다고 말할 때, 우리가 의미하는 것은, 다만 그것의 끝과 경계를 파악할 수 없다는 것일 뿐이다.”라며 토마스 홉스가 말했고, “무한은 한계지울 수 없고 어둡고 경계 없는 바다이다.”라며 존 밀톤이 말했다. 유한의 세계에서는 가장 작은 수와 가장 큰 수가 존재한다. 기원전 500~428년에 살았던 아낙사고라스는 “가장 작은 수와 가장 큰 수는 존재하지 않는다. 다만 모든 수에 대해서 그보다 더 큰 수와 더 작은 수가 존재할 뿐이다.”라며 무한의 세계를 표현하였다.

▲ 무한은, 블랙홀 같은 심연이다 (그림 이무성 한국화가)
기원전 4세기에 제논은 무한에 관해 다음과 같은 ‘제논의 역설’을 내놓았다.
달리기 선수가 한 곳에서 다른 곳으로 움직이려면 그는 우선 그 두 곳 사이의 절반을 달려야 하고, 그 다음 남은 거리의 절반을 달리고, 그 다음 다시 남은 거리의 절반을 달려야 하는데 , 이 과정은 무한히 계속된다. 이것은 무한 번의 과정을 요구하기 때문에 달리기 선수는 절대로 목적 지점에 도착하지 못한다.
제논의 역설은 무한에 관한 두려움을 잘 나타내준다. 물론 제논은 달리기 선수가 유한한 시간이 흐른 후 목적지에 도달할 수 있다는 것을 안다. 하지만 무한이 포함된 위 논증을 설명할 수 없었다.
영(zero)이라는 단어는 ‘비어 있음’ 혹은 ‘공백’을 뜻하는 힌두어 쑨야에서 유래했고, 기호 0은 870년에 만들어진 힌두인의 비문에서 처음 발견 되었다고 한다. 무한을 뜻하는 기호
무한은 17세기 후반 뉴턴과 라이프니츠에 의해서 새롭게 발명된 미적분학의 핵심요소가 되었다. 무한수열에서는 우리가 원하는 만큼 가깝게 거기에 접근하면서도 실제로는 거기에 절대로 도달하지 않게 되는 수를 극한이라 한다.
유한개를 계산할 때는 더하는 순서에 관계없이 항상 같다. 이것을 수의 결합법칙이라 한다. 그러나 무한개의 셈에서는 더하는 순서에 따라 같지 않을 수도 있다. 무한합 1-1+1-1+1- ...에서 합은 다음과 같이 어떻게 더하느냐에 따라 달라질 수 있다.
(1-1)+(1-1)+(1-1)+(1-1)+ ... = 0
1+(-1+1)+(-1+1)+(-1+1)+ ... = 1
이와 같이 무한의 세상에서는 유한의 세상에서 일어날 수 없는 현상이 많이 일어날 수 있다. 무한은 정말 이상한 세상이다. 유한한 세상에 사는 인간이 신은 무한하다고 하는 것은 충분히 이해할 수 있다.
(*) 《수학과 교육》 2014년 106호에 실린 내용을 재구성하였다.

