[그린경제/얼레빗 = 이규봉 교수] 수학자들은 주어진 조건 아래에서 최댓값이나 최솟값을 구하는 문제를 일반적으로 해결하려고 한다. 이러한 방법 중 가장 효율적이라고 알려진 것이 미분적분학이다. 미분적분학에서 가장 기본이 되는 것은 미분(微分)이다. 글자 그대로 미분은 잘게 쪼개는 것이다. 미분을 이해하기 위해 자전거를 타고 언덕을 올라가 보자.
잠깐! 여기에 나오는 수식은 그렇게 어렵지는 않다. 그러나 수식이 신경 쓰이면 따지지 말고 그런가 보다하고 믿고 넘어가기를 바란다. 마치 종교인이 신이 존재함을 믿듯이.
미분이란 변화율이다
자전거를 타고 언덕을 오르면 경사가 급할수록 올라가기가 힘들어진다. 하지만 고개 마루에 도착하면 흘러내린 땀을 닦으며 내려 달릴 기분에 젖는다. 경사가 완만한 곳을 내려갈 때는 브레이크를 잡지 않아도 안전하게 내려갈 수 있으나 경사가 급한 곳은 브레이크를 잡지 않으면 속도가 너무 빨라 큰 사고가 날 수 있다.
경사가 급하다거나 완만하다는 것이 무슨 뜻인가? 앞에 오르막이 있다. 자리에 가만히 서서 고개를 들거나 숙이지 않고 똑바로 앞으로 보았을 때 멀리까지 보이면 경사가 완만한 것이고 가까운 곳이 보이면 경사는 급한 것이다. 다시 말하면 고갯마루를 보기 위해 고개를 쳐들어야만 한다면 높이 쳐들수록 경사는 급하다고 할 수 있다.
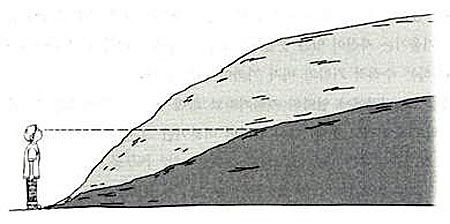
▲ 산을 오를 때 경사가 완만할수록(또는 미분이 작을수록) 멀리 보인다.
두 지점간의 경사는 두 지점 사이의 수평적 길이와 수직적 길이의 비로 생각할 수 있다. 그러므로 경사가 더 급하다고 하는 것은 수평적 길이가 같을 때 수직적 길이가 더 큰 것이다. 즉 일정하게 수평으로 간 거리에서 수직으로 올라간 거리가 크면 클수록 그 언덕은 경사가 급해 올라가기가 힘들고 시간이 많이 걸리나, 반대로 내려갈 때는 쉽고 빠른 시간에 내려갈 수 있다.
결론적으로 두 지점간의 수평적 거리를 x, 수직적 거리를 y라고 하면 경사도(또는 기울기)는 두 거리의 비인 y/x이다. 그런데 문제가 있다. 같은 언덕일지라도 키가 큰 사람이 느끼는 경사도와 작은 사람이 느끼는 경사도가 엄밀하게 말하면 다를 수 있다는 것이다. 즉 키가 큰 사람은 조금 덜 급하게 느끼고 작은 사람은 조금 더 급하게 느낄 것이다. 그렇다고 키 큰 사람이 더 쉽게 언덕을 오르는 것은 아니다. 왜냐하면 실제 언덕의 기울기는 누가 보든지 같기 때문이다. 두 지점 사이의 거리를 눈의 위치에서 보지 말고 발에서부터 생각하면 언덕의 기울기는 모두 같게 느껴진다.
또 다른 문제는 똑같은 언덕이라도 언덕이 반듯하게 똑바로 올라가지 않는 한 올라가면서 급한 곳도 있고 완만한 곳도 있는 것이다. 그래서 언덕 아래와 언덕 위 두 지점 사이의 기울기보다 자기가 서 있는 곳에서의 기울기를 생각해 볼 수 있다. 이 기울기는 자신이 있는 곳을 중심으로 수평적 거리가 점점 작아질 때 그것에 대응하는 수직적 거리의 비가 가까이 가는 값이다.
이것을 그 지점에서 언덕의 기울기라고 하며 이 기울기의 값을 그 지점에서 언덕길의 미분이라고 한다. 다시 말하면 미분이란 그 점에서의 변화율을 뜻하는 것이다. 어느 순간 미분이 크다는 것이나 그 순간에 변화가 크게 일어난다는 것이나 같은 의미이다.
미분을 이용하면 최댓값을 쉽게 구할 수 있다. 예를 들어 농부가 자기 농장에 둘레가 40m가 되는 직사각형 모양의 밭을 만들려고 하는 데, 가능한 그 면적이 최대가 되게 하려면 어떤 직사각형으로 만들어야 할까?
한 변의 길이를 x라고 하면 둘레가 40m이므로 직사각형 모양의 밭의 다른 한 변의 길이는 20-x이다. 따라서 그 땅의 면적은 x(20-x)이다. 이 문제는 x(20-x)가 가장 큰 값이 되는 x를 구하는 것과 같다. 그러므로 y=x(20-x)=-x2+20x라고 하면 이 문제는 y가 최댓값이 되는 x를 찾는 것과 같다.
미분을 사용하지 않고 구하면 y=-x2+20x=-(x-10)2+100 이므로 x=10일 때 최댓값은 100이다. 다시 말하면 밭의 면적 (y)은 한 변의 길이(x)가 10일 때 최대가 되어 밭은 정사각형으로 만들어야 최대의 면적을 갖는다.
미분을 이용하면 이 문제를 더 쉽게 구할 수 있다. y가 최댓값이 되는 x는 y를 x에 관해 미분한 y’=-2x+20 이 0이 될 때이다. 따라서 x=10이 된다. 즉 한 변의 길이를 10으로 하는 직사각형, 곧 정사각형을 만들면 면적은 100으로 최대가 된다.
맥주거품은 왜 사라지거나 터질까?
2012년 말에 생맥주에 대한 기사가 나왔다. 호프집에서 마시는 생맥주가 주문하는 대로 그 양이 다 나오지 않고 그것보다 항상 적게 나온다는 것이다. 그것도 최대 23퍼센트나 적게. 다시 말하면 500시시를 주문하면 한 435시시 정도만 나온다는 것이다. 병맥주나 깡통맥주와 달리 잔에 담아 내오는 생맥주는 그 양을 확인할 길이 없다. 잔의 용량에 따라 주문할 뿐이고 잔의 용량만큼 그렇게 나오는 줄 알고 있었다. 그런데 이 잔 조차도 정확하지 않다는 것이다.
생맥주를 담는 용기는 보통 500시시, 750시시, 1000시시, 2000시시, 3000시시 등이 있다. 소비자보호원이 용기의 용량을 측정해보았더니 가장 많이 사용하는 500시시의 잔은 그런대로 용량이 정확했으나 2000시시나 3000시시는 용기 자체의 용량이 부족한 것으로 드러났다. 결국 불신으로 인해 이제는 생맥주도 용량이 표시된 잔이나 용기에 담아 마시게 될 것 같다.
맥주는 거품이 많다. 특히 생맥주는 위에 깔린 거품과 함께 마신다. 잔에 놓인 맥주 거품을 보면 뽀글뽀글 올라오면서 점점 커져 터지기도 하고, 어떤 작은 거품알갱이는 점점 작아져 사라지기도 한다. 마시지 않고 가만 놔두면 거품이 모두 사라져 그야말로 김빠진 맥주가 된다. 왜 큰 거품은 점점 커져 터지고 작은 거품은 점점 작아져 사라질까?

▲ 맥주거품은 왜 점점 커져 터지거나 점점 작아져 사라질까? (그림 이무성 한국화가)
맥주에 거품이 나는 것은 맥주를 담은 용기에 이산화탄소가 들어있기 때문이다. 이산화탄소는 액체로 녹아있는 것보다 기체로 있는 것이 훨씬 더 안정된다. 그래서 이산화탄소가 과포화상태로 용기에 담겨있는 탄산음료는 뚜껑이 열리면 이산화탄소가 거품과 함께 나온다. 거품과 액체 사이에는 표면장력이 작용하고 거품이 갖고 있는 에너지는 거품의 부피가 커질수록 작아지고 거품의 겉넓이가 클수록 비례하여 커진다고 한다. 한편 거품알갱이는 되도록 작은 에너지를 가지려고 한다는 것이다.
반지름이 r인 공의 부피는 4πr3/3이고 표면적은 4πr2이다. 거품이 갖고 있는 에너지는 거품의 부피가 커질수록 작아지고 거품의 겉넓이가 클수록 비례하여 커지므로 거품이 갖는 에너지는 E(r)=-a(4πr3/3)+b(4πr2)와 같이 나타낼 수 있다. a, b는 적당한 양수이다.
설명하기 편하게 계수를 모두 지우고 단순히 E(r)=-r3+3r2 라고 하자. 이 함수를 미분하면 다음과 같다.
E'(r)=-3r2+6r=-3r(r-2)
따라서 r=0과 2에서 거품이 갖는 에너지를 미분한 값이 0이 된다. r=0란 의미는 이미 거품이 아니므로 r=2에서 거품은 최댓값 또는 최솟값을 갖는다. 이 문제의 경우 r=2에서 최댓값을 가지므로 이 거품은 반지름의 크기가 2일 때 최대의 에너지를 가진다.
거품알갱이는 되도록 작은 에너지를 가지려는 경향이 있기 때문에 반지름이 2보다 작은 알갱이는 더 커지지 않고 점점 작아져 사라진다. 2보다 큰 거품알갱이는 에너지가 더 작아지려면 반지름이 2보다 더 커져야 하므로 거품이 점점 커져 수면으로 올라가 터지게 되는 것이다. 그래서 잔에 놓인 맥주 거품은 뽀글뽀글 올라오면서 점점 커져 터지기도 하고, 작은 거품알갱이는 점점 작아져 사라진다.
다음 편에 독점행위를 왜 법으로 금지해야만 하는지 미분의 성질을 이용해 알아본다.

