[그린경제/얼레빗=이규봉 교수]  수학에서 부딪치는 어려운 문제를 해결하는 방법으로 변환-풀이-역변환 기법(transform- solve-invert technique)이 있다. 말 그대로 어려운 문제를 쉬운 문제로 변환해서 해결한 후 다시 반대로 변환하는 방법이다. 이러한 방법은 실생활에서도 많이 사용된다.  

예를 들어 보자. 우리는 살면서 스스로 해결하기에 어려운 문제에 부딪치면 어떻게 이 문제를 해결하는 것이 좋을까? 어렸을 때는 가장 좋은 방법이 부모한테 떼쓰는 것이다. 이처럼 우선은 이 문제를 해결할 수 있는 사람이나 환경으로 가져가서 도움을 청할 것이다. 그렇다고 도움을 요청하고는 마치 자신의 일이 아닌 것처럼 그 문제를 내팽기지는 않을 것이다. 남의 도움을 받아 그 문제를 해결한 후 도움을 받은 것에 대해 나중에 갚으면 된다.  

우리는 인생을 살면서 이런 방법을 많이 쓴다. 사회는 서로 돕고 살아야 하기 때문이다. 자존심이 너무 세어 남의 도움을 전혀 받지 않으려고 하는 것은 좋지 않다. 이것은 자신 역시 남에게 도움을 주지 않겠다는 것과 같기 때문이다. 그러므로 당장 자신이 혼자 해결할 수 없다고 무작정 포기하는 것은 옳지 않다.  

지금 집이 꼭 필요하다고 하자. 그런데 저축한 돈이 집을 살 정도로 충분하지는 않다. 그러면 충분한 돈을 모을 때까지 집 사는 것을 미루어야 하겠는가? 물론 그것도 방법은 될 수 있다. 그러나 집이 지금 당장 필요하면 어떻게 해야 할까? 방법이 있다. 필요한 자금을 은행에 자신이 사고 싶은 집을 저당 맡기고 융자를 받아서 집을 사면된다. 단 자신의 수입에 맞추어 충분히 갚을 수 있을 정도로 빌려야 한다.  

그런 뒤 저축을 하여 이자를 포함해서 기간 안에 갚으면 된다. 이것 역시 전형적인 변환-풀이-역변환 기법이다. 돈이 모자란 문제를 은행에 가져가는 것이 변환에 해당하고, 은행에서 융자를 받아 집을 사는 것이 풀이에 해당하며 나중 이자와 함께 융자를 갚는 것이 역변환에 해당한다.

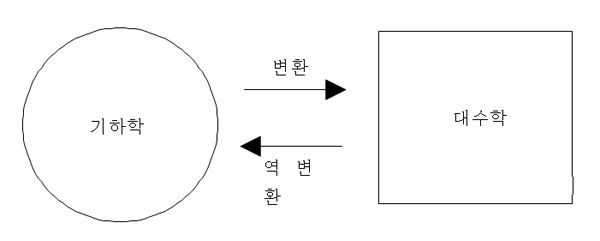
기하와 대수의 관계 

실수의 모든 수는 직선의 모든 점과 일대일 대응이다. 다시 말하면 실수 각각을 직선 위에 표시할 수 있고 직선 위의 모든 점을 실수로 나타낼 수 있다. 여기서 실수는 대수학을 대표하고 직선은 기하학을 대표한다. 마찬가지로 실수 두 개를 순서 있게 나열한 순서쌍 (a,b)와 평면 위의 점 P 사이에도, 그리고 실수 세 개를 순서 있게 나열한 순서쌍 (a,b,c)와 공간위의 점 Q 사이에도 역시 일대일 대응이 성립된다.  

그러므로 평면 위의 곡선은 방정식 f(x,y)=0으로 표시되고 그리고 공간 위의 곡선은 방정식 f(x,y,z)=0으로 표시할 수 있다. 각 방정식을 만족하는 순서쌍은 각각 평면 그리고 공간 위의 점에 대응된다. 따라서 기하학적인 문제와 대수적인 문제는 서로 도우며 문제를 해결한다. 

기하학의 문제는 그에 대응하는 대수학의 문제로 변환되고, 대수적 문제를 푼 다음 그 문제를 기하학 문제로 다시 역변환하여 기하학 문제의 해를 구할 수 있다. 예를 들면 직선의 문제는 y=ax+b와 같은 방정식으로, 원의 문제는 x2+y2=r2과 같은 방정식으로 변환할 수 있다. 

변환-풀이-역변환 기법이란 어려운 문제를 그와 동치이면서 더 알기 쉬운 문제로 변환한(transform) 뒤, 그 쉬운 문제를 풀어서(solve) 나온 답을 원래의 문제로 역변환(invert)하여 해를 구하는 방법을 말한다. 다시 말하면 변환-풀이-역변환 기법은 주어진 수학적인 상황을 보다 쉬운 상황으로 변화시키고 쉬운 상황에서 해를 구한다. 그리고 원래의 상황에 맞는 답을 얻기 위해서 그 변환을 역변환 시키는 방법이다. 

방정식의 근 구하기 

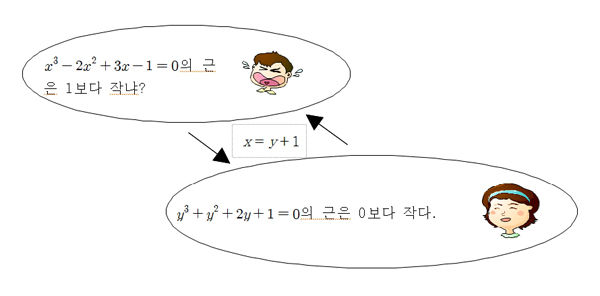
3차방정식 x3-2x2+3x-1=0을 살펴보자. 이 방정식의 왼쪽 항에 적당한 수 x를 대입해서 그 값이 0이 되면 우리는 x를 이 방정식의 해(solution) 또는 근(root)이라고 한다. 문제는 이 방정식의 근이 1보다 작다는 것을 보이는 것이다. 가장 쉬운 방법이라 생각할 수 있는 3차방정식의 근의 공식을 이용할 수 있겠으나 일반적으로 이 공식은 잘 모른다. 그래서 이 방정식을 그대로 두고 생각하면 짜증나고 그러다 보면 수학이 싫어지게 된다. 그러나 순간에 번뜩이는 생각이 떠올라 x 대신 y+1를 이 방정식에 대입하면 이 방정식과 동치인 새로운 방정식 

y3+y2+2y+1=0 

으로 변환된다. y=x-1이므로 주어진 방정식의 근 x가 1보다 작은 것은 이 새 방정식의 근 y가 0보다 작다와 같음을 알 수 있다. 그런데 새 방정식의 계수가 모두 양수이므로 0과 같거나 아니면 더 큰 어떤 수 y도 이 방정식의 왼쪽 항에 대입하면 결코 0이 될 수 없음을 알게 된다. 다시 말하면 이 새 방정식이 성립하려면 y의 값은 음수가 되어야 한다는 것이다.  

곧 변환된 새로운 방정식의 해 y는 0보다 작음을 알 수 있다. y의 값이 0보다 작다는 사실을 다시 역변환하면 x=y+1이므로 x은 1보다 작음을 알 수 있다. 따라서 주어진 방정식의 근 x은 1 보다 작다는 것을 보이게 된다.

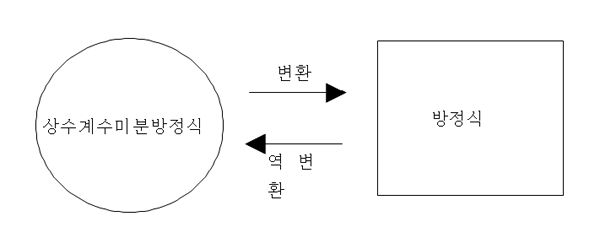
미분방정식의 해법에서 상수계수 미분방정식은 보조방정식을 이용하여 보다 쉬운 방정식으로 변환하여 해를 구할 수 있다. 또한 미분방정식을 라플라스 변환하면 보다 쉬운 방정식이 된다. 이 방정식의 해를 구한 뒤 다시 그 값을 역변환 하여 미분방정식의 해를 구한다. 

상수계수미분방정식 ay''+by'+cy=0의 일반해를 구하는 것은 2차방정식의 근을 구하는 것과 같다. 위 미분방정식에서 a, b, c는 수를 대신하며 이를 계수라고 말한다. 위 미분방정식의 계수를 이용해 2차방정식 am2+bm+c=0을 만든다. 2차방정식의 근은 미분방정식의 근보다 더 쉽게 구할 수 있다. 이 2차방정식의 두 근을 m1, m2(또는 m)라고 하면 주어진 미분방정식의 해는 다음과 같이 구할 수 있다.  

(1) m1과 m2가 다르면 y=c1exp(m1x)+c2exp(m2x)
(2) m1과 m2가 같으면(m이라 하자) y=(c1+c2x)exp(mx)
(3) m1과 m2가 복소수로 α+iβ, α-iβ이면 y=exp(αx){c1cos(βx)+c2sin(βx)} 

여기서 c1과 c2는 임의의 수로 어떤 수를 대입해도 성립한다. 예를 들면 미분방정식 y''-y'-6y=0의 보조방정식은 미분방정식의 계수가 차례로 1, -1, -6이므로 m2-m-6=0이 된다. m2-m-6=(m-3)(m+2)이므로 2차방정식의 해는 2와 -3이다. 따라서 미분방정식 y''-y'-6y=0을 만족하는 해는 (1)에 의해서 y=c1exp(-3x)+c2exp(2x)이 된다.