[그린경제/얼레빗=이규봉 교수]  종교를 믿는 사람들에게는 대체로 자신이 믿는 절대자란 이 세상에 존재하지만 그 실체는 보이지 않는다고 믿고 있다. 그러나 성경에 따르면 하느님은 예수라는 인간의 형태로 이 세상에 태어나 그 실체를 보여주었다. 그러나 그가 죽고 부활한 뒤에는 아직까지는 그러한 일이 없고 단지 재림하기를 기다리고 있다 

디락 델타 함수 δ(t-t0)는 t0를 제외한 모든 수에서는 0이고 t0에서는 정의되지 않아 그 실체는 볼 수가 없지만, 적분한 값은 항상 존재하므로 그 존재감은 분명히 있다. 따라서 디락 델타 함수는 이 세상 어느 곳에서나 존재하는 절대자로 생각할 수 있다. 우리 인간은 유한한 존재이므로 함수 g는 신앙을 가진 모든 사람을 나타내어 g(t)는 어떤 지점 t에서 그 사람이 하는 행동을 보여준다. 

참다운 신앙을 가졌다는 것은 자기가 믿는 절대자를 믿고 마음에 품은 것이므로 그 사람 g가 있는 곳 t0에서 신자로서 보여주는 행동은 절대자와 함께 하는 마음으로 ∫δ(t-t0)g(t)dt이 된다. 그런데 ∫δ(t-t0)g(t)dt=g(t0)이므로 절대자의 실체는 보이지 않고 그의 행동만 보인다.

곧 절대자는 자신을 믿는 그 사람을 통해 우리에게 자신의 모습을 보여준다. 절대자는 변하지 않는다. 다만 사람과 장소가 다를 뿐이다. 각자의 행동이 자신이 믿는 종교의 내면을 보여주는 것이다. 따라서 자신의 행동이 올바르지 못하면 그것은 자신이 믿는 종교를 욕되게 하는 것이다. 그러나 자신이 올바른 행동을 하면 다른 사람은 그러한 행동을 보고 그 종교를 믿게 되는 것이다. 

우리가 신앙을 갖는다는 것은 우리의 몸과 행동을 통하여 우리가 믿는 그 분의 생각을 나타내는 것이다. 이것을 잘 나타낸 성경 구절이 마태오 5장 16절이다. 

너희의 빛이 사람들 앞을 비추어 그들이 너희의 착한 행실을 보고 하늘에 계신 너희 아버지를 찬양하게 하여라. 

예수의 삶 그 자체가 하느님을 보여주는 것이다. 사람들은 예수가 하는 행동을 보고 그가 믿는 하느님을 믿게 된다. 예수는 헐벗은 이웃을 위해 살았다. 그러기 위해서 자신들이 거룩하고 깨끗하다고 믿는 당시 기득권 세력에 대항하게 됐고 결국 십자가에서 처형됐다.  

이 세상에는 거짓된 신앙인이 너무도 많다. 어느 종교든지 살인을 금하고 있다. 절대적으로 금하고 있다. 그럼에도 불구하고 그럴싸한 핑계를 대며 자신들이 믿는 신의 이름으로 살인을 하거나 또는 살인하게 만드는 무리들이 너무도 많다. 

진실된 신앙인일수록 자신이 믿는 그 분이 행동하는 것처럼 보이도록 노력해야 할 것이다. 종교를 불문하고 으뜸인 신앙의 가르침은 이웃 사랑이다. 당신이 이웃을 사랑할 때 당신의 모습을 통해 당신이 믿는 절대자의 모습이 나오는 것이다.

▲ 다일공동체 최일도 목사가 사랑의 실천을 하고 있다.

그렇다면 디락 델타(Dirac delta) 함수가 무엇인지 설명하자. 고등학교 과정의 수학이 포함되니 처음에 나오는 수학적인 용어에 대해 조금 참고 곰곰히 생각해보며 읽으면 이해가 되리라 본다. 

면적이 1인 직사각형이 있다. 면적이 변하지 않는다면 밑변이 점점 작아짐에 따라 높이는 점점 커진다. 즉 밑변의 길이가 1이면 높이는 1이 되고, 밑변의 길이가 1/2이 되면 높이는 2가 된다. 일반적으로 밑변의 길이가 2a이면 높이는 1/(2a)이 된다. 밑변의 길이에 따라 높이가 달라지므로 이 직사각형의 높이는 밑변의 길이에 대응하는 함수가 된다.  

점 t0를 중심으로 반경 a인 구간 (t0-a, t0+a)을 밑변이라고 하자. 그러면 밑변의 길이는 2a이다. 따라서 높이는 이 구간 위에서는 1/(2a)이고 그 밖에서는 0이 된다. 이것을 y=δa(t-t0)라고 나타낸다. 그러면 이 함수로 둘러싸인 직사각형의 면적은 a와 t0에 관계없이 항상 1이다.  

a가 0으로 가까이 가면 이 함수는 점차 t0을 제외한 모든 곳에서 0이 되고 0에서는 그 값이 너무 커져 존재하지 않게 된다. 다시 말하면 t0=0인 경우 y=δa(t)는 (-a,a)에서 함수값이 1/(2a)이 되어 a가 점점 작아질수록 그래프는 다음과 같이 0이 아닌 구간은 점점 좁아지나 그곳에서 함수값은 점점 커진다. 

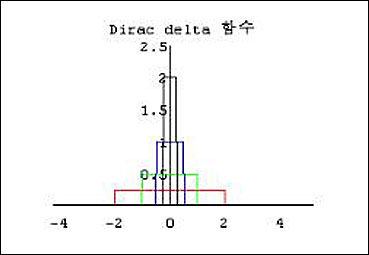
▲ 구간이 작아질수록 커지는 디락 델타 함수의 그래프

디락 델타 함수가 t0에서 유한하고 끊어지지 않은 함수 g(t)와 만나면 자신의 존재를 t0에서 g(t)의 함수값 g(t0)로 다음과 같이 나타낸다[의심하지 말고 이 아름다운 공식을 음미하라]. 

∫δ(t-t0)g(t)dt=g(t0) 

미친 운전사로부터 핸들을 빼앗아야 한다 

독일의 성직자 본회퍼(Dietrich Bonhoeffer, 1906~1945)는 1933년 히틀러가 권력을 잡고 있을 때 라디오 방송을 통해 국민들을 잘못 인도할 지도자가 될 수 있는 지도자를 우상처럼 떠받드는 우상숭배의 위험성을 경고하며 나치 정권에 대항하였다. 그는 다음과 같이 말하면 히틀러 암살을 꾸미는 반나치 저항 운동에 가입했다. 

만일 어떤 미친 운전사가 사람들이 많이 다니는 인도 위로 차를 몰아 질주한다면 목사인 나는 희생자들의 장례나 치러주고 가족들을 위로하는 일만 하는 것이 나의 유일한 임무라 생각하지 않습니다. 나는 그 자동차에 뛰어올라 그 미친 운전사로부터 핸들을 빼앗아야 할 것입니다. - 오강남, <종교, 심층을 보다>, 현암사, 2011, 245쪽 
 

▲ 《종교, 심층을 보다》, 오강남, 현암사

성직자로서 그는 암살 음모에 가입하는 것 자체가 죄가 되지만 그 죄를 다른 사람과 다음 세대를 위해 어쩔 수 없이 자기가 떠맡아야 한다고 생각했다. 체포된 본 회퍼는 1945년 4월에 교수형을 당했다. 그의 사상은 그리스도가 나를 위해서라기보다는 우리를 위해, 결국에는 남을 위해 사신 분이라며 남을 위한 존재라는 점을 강조하였다. 

값싼 은혜는 우리 교회의 치명적인 적이다. 오늘 우리의 싸움은 값비싼 은혜를 얻기 위한 싸움이다. 값비싼 은혜는 예수의 십자가를 지고 가는 것인데, 값싼 은혜는 예수의 십자가를 타고 가려는 것이라 할 수 있다. - 오강남, <종교, 심층을 보다>, 현암사, 2011, 245쪽 

* 《수학과 교육》 2014년 105호에 실린 내용을 재구성하였다.
   일부 수학 기호가 컴퓨터 운영체제 문제로 제대로 표기되지 않았습니다. 양해 바랍니다.