[그린경제/얼레빗=이규봉 교수] 지리산 둘레를 걸으면서 지리산의 정취와 옹기종기 모여 있는 마을을 돌아볼 수 있는 둘레길이 만들어졌고, 제주 둘레를 걸으면서 제주만의 독특한 맛을 느낄 수 있는 올레길이 만들어졌다. 이러한 길이 인기를 끌면서 전국에 산책길을 만드는 것이 유행이 되었다. 등산을 한다면 반드시 산 정상을 올라가야 하는 것으로 알고 있었으나 이제는 주변을 산책하며 소통하는 것이 중요하게 되었다. 그러자 제주 올레길의 모델이 된 프랑스에서 스페인으로 넘어가는 일명 산티아고로 가는 길(Cameno de Santiago)이 관심을 끌고 있다. ▲ 지리산 둘레길 1 (남원시 제공) ▲ 지리산 둘레길 2 (남원시 제공) 산티아고로 가는 길 한 달을 넘게 걸어야 완주할 수 있어 끈기를 요구하는 이 낭만적인 산티아고로 가는 길에는 역사적인 슬픔이 있다. 이 길은 9세기 초 아스투리아스 왕국의 알폰소 2세가 예수의 형제로 알려진 성 야고보의 무덤에 성당을 세우고, 야고보를 스페인의 수호성인으로 봉하면서 유럽에 알려졌다. 유럽 기독교 국가들의 시민들이 성지 순례에 나서면서 자연스레 이베리아 반도를 지배하고 있던 이슬람 세력을 축출하기 위한 국토수복운동(Re
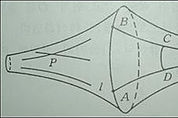
[그린경제/얼레빗=이규봉 교수] 러시아의 수학자 로바체프스키는 1829년 비유클리드 기하학에 관한 최초의 논문 기하학의 원리에 관하여를 러시아어로, 1840년 평행선 이론에 대한 기하학적 연구를 독일어로 발표하였다. 여기서 그는 평행선의 존재를 하나 이상으로 가정하였다. 헝가리의 볼리야이도 로바체프스키와는 독립적으로 1832년 만일 한 점을 지나 주어진 직선과 평행인 직선이 하나 이상 있다라는 가정 하에 모순이 없는 새로운 기하학을 발표했다. 이 논문은 엄청난 비판을 받았을 뿐 아니라 이미 3년 전에 로바체프스키가 러시아 잡지에 발표했음을 알고 볼리야이는 정신적 우울증에 빠져 더 이상 연구를 발표하지 않았다. 독일의 가우스도 독립적으로 볼리야이가 의문을 제기하기 전에 이미 새로운 기하학을 알고 있었다. 그러나 그는 전혀 연구 결과를 발표하지 않았고 그의 사후에 알려지게 되었다. 삼각형의 내각의 합은 180도보다 작다 유클리드 기하학의 평행공준 대신 한 점을 지나고 주어진 직선에 평행한 직선은 두 개 이상 존재한다.라는 가정아래 생성된 기하학을 로바체프스키 기하학이라 한다. 이 기하학이 성립하는 모형으로 공의 안쪽이나 나팔의 겉 표면을 들 수 있다. 아래 그
[그린경제/얼레빗=이규봉 교수] 조선시대 청백리의 대명사인 황희 정승에게는 다음과 같은 일화가 있다. 어느 날 황희 정승이 사랑방에서 책을 읽고 있었는데 밖에서 계집종 둘이 악을 쓰고 다투고 있었다. 황희가 밖으로 내다보자 원체 마음이 너그러운 주인인지라 다투던 계집종 중 예쁜이가 쪼르르 달려가 사실을 일러바치며 자신이 옳지 않냐고 물었다. 그러자 황희는 고개를 끄덕이며 그래 네가 옳다고 답을 했다. 그러자 다른 계집종 곱단이가 다시 그에게 달려가 자초지종을 설명했다. 그러자 황희는 또 다시 고개를 끄덕이며 너 역시 옳구나 했다. 그러자 옆에서 이를 지켜보던 황희 정승의 부인이 어처구니가 없어 한 쪽이 옳으면 다른 한 쪽이 그른 일이 아닙니까? 나라 정치도 그와 같이 하면 어떻게 되옵니까?하니 황희 정승은 또 다시 고개를 끄덕이며 당신 말도 옳소라고 대답했다. ▲ 그림 이무성 한국화가 이와 같은 황희 정승의 말을 이도저도 아닌 말장난일 뿐이라며 비난하는 사람도 많다. 그러나 황희 정승의 대응은 다툼을 피해가는 매우 현명한 일이다. 상대방의 입장을 잘 이해하면 그가 특별히 나쁜 사람이 아닌 한 그의 말도 일리가 있는 것이다. 이것을 역지사지(易地思之)라
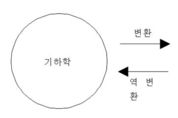
[그린경제/얼레빗=이규봉 교수] 수학에서 부딪치는 어려운 문제를 해결하는 방법으로 변환-풀이-역변환 기법(transform- solve-invert technique)이 있다. 말 그대로 어려운 문제를 쉬운 문제로 변환해서 해결한 후 다시 반대로 변환하는 방법이다. 이러한 방법은 실생활에서도 많이 사용된다. 예를 들어 보자. 우리는 살면서 스스로 해결하기에 어려운 문제에 부딪치면 어떻게 이 문제를 해결하는 것이 좋을까? 어렸을 때는 가장 좋은 방법이 부모한테 떼쓰는 것이다. 이처럼 우선은 이 문제를 해결할 수 있는 사람이나 환경으로 가져가서 도움을 청할 것이다. 그렇다고 도움을 요청하고는 마치 자신의 일이 아닌 것처럼 그 문제를 내팽기지는 않을 것이다. 남의 도움을 받아 그 문제를 해결한 후 도움을 받은 것에 대해 나중에 갚으면 된다. 우리는 인생을 살면서 이런 방법을 많이 쓴다. 사회는 서로 돕고 살아야 하기 때문이다. 자존심이 너무 세어 남의 도움을 전혀 받지 않으려고 하는 것은 좋지 않다. 이것은 자신 역시 남에게 도움을 주지 않겠다는 것과 같기 때문이다. 그러므로 당장 자신이 혼자 해결할 수 없다고 무작정 포기하는 것은 옳지 않다. 지금 집이 꼭
[그린경제/얼레빗=이규봉 교수] 본래무일물(本來無一物)이란 말이 있다. 본래부터 있었던 물건은 없다는 뜻이다. 이 세상에 태어날 때 아무것도 갖고 오지 않았고 이 세상에서 사라져 갈 때도 역시 빈손으로 간다는 것이다. 법정스님은 괴로움은 집착에서 온다. 아무것도 갖지 않을 때 온 세상을 갖게 된다는 것은 무소유의 또 다른 의미이다.라며 말한다. 영원히 결혼하지 않고 혼자 사는 총각에게 왜 그렇게 혼자 사나?하고 그 이유를 물으니 나에게 여자가 없으니 이 세상 모든 여자가 내 여자 아닌가?라고 답한다. 노숙자에게 왜 집이 없이 노숙하고 지내나?고 물으니 내가 가진 땅과 집이 없으니 이 세상 땅과 집이 다 내 것이 아니겠는가?라며 답한다. 마치 이들은 이미 무소유의 개념을 아는 것 같다. ▲ ≪버리고 떠나기≫, 법정, 샘터사, 2001 법정스님은 ≪버리고 떠나기≫에서 잃는다는 것이 잘못된 것도 나쁜 것만도 아니다라고 말한다. 때로는 잃지 않고는 얻을 수가 없다. 크게 버릴 줄 아는 사람만이 크게 얻을 수 있다. 전체가 되기 위해서는 일단 없어야 한다고 말한다. 무엇이든지 차지하고 채우려고만 하면 사람은 거칠어지고 무디어진다. 맑은 바람이 지나갈 여백이 없
[그린경제/얼레빗=이규봉 교수] 지금은 입적하신 법정스님께선 생전에 많은 책을 저술해 많은 중생에게 따뜻한 감정을 불어놓으셨다. 스님의 책을 대표하는 것이 무소유다. 1976년에 초판이 나와 지금까지 가장 많이 읽힌 책이다. 필자도 대학생 시절 처음 이 책을 접했고 지금도 간간히 꺼내 보곤 한다. 이 책에서 스님이 길을 떠나는데 갑자기 집에서 기르던 난초를 아침에 양지바른 곳에 잠깐 내 놓은 것이 생각나 되돌아 왔다고 한다. 난초는 오랫동안 햇빛을 받으면 죽을 수도 있기 때문이다. 그리고는 깨달은바 난초를 남에게 주었다고 하며 다음과 같이 말한다. ▲ ≪무소유≫, 법정, 범우사 우리들이 필요에 의해서 물건을 갖게 되지만, 때로는 그 물건 때문에 적잖이 마음이 쓰이게 된다. 그러니까 무엇을 갖는다는 것은 다른 한편 무엇인가에 얽매인다는 뜻이다. 필요에 따라 가졌던 것이 도리어 우리를 부자유하게 얽어맨다고 할 때 주객이 전도되어 우리는 가짐을 당하게 된다. 그러므로 많이 갖고 있다는 것은 흔히 자랑거리로 되어 있지만, 그만큼 많이 얽혀 있다는 측면도 동시에 지니고 있다. - 법정, ≪무소유≫, 범우사, 2010, 22쪽 필요 이상으로 많이 가지면 오히려 불
[그린경제/얼레빗 = 이규봉 교수] 나는 2003년 7월에서 다음 해 7월까지 뉴질랜드 남섬의 중심 도시인 크라이스트쳐어치의 캔터베리대학교에서 방문교수로 지냈던 적이 있었다. 뉴질랜드의 자연은 거의 훼손되지 않고 잘 보존되어 있었으며 많은 지역이 원시 그대로 보존되어 있었다. 우리나라는 자연환경을 파괴하면서 경제적 이득을 취하는데 반해 뉴질랜드는 자연환경을 보존하면서 관광을 나라의 주요한 정책으로 삼아 경제적 이득을 취하고 있었다. 결과적으로 뉴질랜드의 후손들은 그들의 선조가 남긴 자연환경의 혜택을 계속 볼 수 있겠지만 우리나라의 후손들은 그들의 선조가 잘 먹고 남긴 쓰레기를 청소하느라 힘든 세월을 보낼 것 같은 걱정이 들었다. 마라톤을 완주하다 남북한 모두 합한 우리 땅보다 좀 더 큰 영토에 우리의 1/20도 채 안 되는 인구가 살고 있으니 그들의 생활은 바쁜 것 하고는 멀었다. 주민들은 여유가 있어 보였고 삶을 즐기는 것 같았다. 푼돈으로 골프를 즐길 수 있고 주말이면 늘 다양한 스포츠가 곳곳에서 행해졌다. 이른바 레저 스포츠의 천국이다. 맥주회사가 주관하는 2월에 열린 스파이츠의 해안과 해안 삼종 경기(Speight's Coast to Coast Mul
[그린경제/얼레빗 = 이규봉 교수] 산악자전거 엘파마 티타니아의 예를 들어 보자. 수동식 자동차에서는 고속으로 달릴 때는 5단으로 달리고 저속이고 힘이 필요할 때는 1단으로 달린다. 즉 속도가 빠를수록 기어의 단 수를 올리고 힘이 더 필요할수록 내린다. 이에 맞추어 자전거에서도 각 톱니의 수의 크기에 따라 다음과 같이 숫자를 부여하자. 다음 표를 보면 페달을 한 번 돌리는데 3단-9단 기어비는 가장 높은 회전비로 페달을 한 번 돌릴 때 뒷바퀴는 4번 회전되나, 1단-1단 기어비는 가장 낮은 회전비로 반 바퀴 조금 더 돈다. 위 표를 보면 엇비슷한 회전비가 있다. 예를 들면 2단X9단의 회전비는 3단X7단과, 그리고 2단X8단은 3단X6단과 거의 비슷하다. 앞 기어는 자전거 프레임을 기준으로 바깥쪽이 큰 기어(3단)이고, 뒷 기어는 바깥쪽이 가장 작은 기어(9단)이다. 그러므로 앞 기어의 바깥쪽과 뒷 기어의 안쪽 또는 앞 기어의 안쪽과 뒷 기어의 바깥쪽을 연결하면 체인이 크게 비틀리게 된다. 그러므로 1단X9단이나 3단X1단 같은 기어의 조합은 굳이 사용할 필요가 없다. 그와 비슷한 회전비를 갖는 다른 기어 조합을 이용하면 된다. 앞 기어의 가장
[그린경제/얼레빗 = 이규봉 교수] 2008년 2월에 제대를 막 한 아들과 함께 보름 동안 타이완에 자전거 여행을 간 적이 있다. 공항 인근에서 하룻밤을 지내고 해안을 따라 시계 반대 방향으로 가는 여행이었다. 서해안은 밋밋하기 그지없었으나 남쪽 끝에 있는 켄팅(墾丁) 국립공원을 시작으로 동해안의 거의 모든 길은 절경이었다. 북부해안을 지나 서해안으로 오면 딴수이(淡水)라는 도시가 나온다. 이 도시에서 하구를 따라 발리(八里)까지 15km의 자전거 전용도로가 설치되어 도시와 도시를 연결하였다. 정말 경치 좋은 곳에 보행자와 자전거를 위한 이 길은 사람과 자전거가 다니는 길이 완전히 분리되어 있을 뿐 아니라 오토바이는 들어올 수 없도록 저지대를 만들어 놓았다. ▲ 딴수이에서 발리까지 자전거 전용도로 자전거를 타자 당시만 해도 우리나라에는 제대로 된 자전거 길이 없었다. 타이완의 이러한 자전거 길이 부러워 대전을 중심으로 하는 인터넷 신문인 디트뉴스에 기사를 쓴 적이 있다. 여기에서 우리나라도 도시와 도시를 연결하는 끊어지지 않은 자전거 전용도로가 있었으면 좋겠다고 썼다. 그 후 5년이 지난 2003년 우리나라에는 상상도 못한 자전거 길이 생겼다. 내가 기대
[그린경제/얼레빗 = 이규봉 교수] 컴퓨터가 매우 실용화되면서 종이의 소비가 줄어들 것으로 기대했다. 그러나 화면 속의 글씨보다는 종이 위에 인쇄된 글씨가 보기 편해 출력을 또 하기도 한다. 중요한 자료의 보관을 위해서는 디지털 저장 뿐 아니라 고전적인 인쇄물로 저장하는 습관도 아직 갖고 있다. 특히 컴퓨터의 인쇄술 발전은 홍보물을 값 싸게 남발하여 종이의 소비를 크게 줄이지는 못했다. 종이를 소비하는 것은 나무를 벌목하는 것이나 다름없어 이는 환경에 매우 나쁜 영향을 끼친다. ▲ 복사용지들 미국을 제외한 대부분의 나라에서는 같은 규격의 컴퓨터 용지를 사용한다. A와 B로 시작하는 종이가 그것이다. 이 종이에는 일정한 특징이 있다. 그것은 비록 크기가 다를지라도 모양이 같다는 것이다. 모양이 같다는 것은 닮은꼴로 적당한 비율로 축소하고 확대하면 서로 다른 규격의 종이로 출력할 수 있다. 따라서 닮은꼴은 종이의 낭비를 막아줄 수 있다. 여기에 숨어 있는 수가 있으니 바로 2의 제곱근인 2이다. 이 수의 크기는 밑변과 높이가 1인 직각삼각형의 빗변의 길이와 같다. 복사용지에 숨겨진 수 우리가 주로 사용하는 복사용지는 A4나 B4 또는 B5를 많이 사용한다.
서울시 영등포구 영신로 32. 그린오피스텔 306호 | 대표전화 : 02-733-5027 | 팩스 : 02-733-5028
발행·편집인 : 김영조 | 언론사 등록번호 : 서울 아03923 | 등록일자 : 2015년 10월 6일 | 발행일자 : 2015년 10월 6일 | 사업자등록번호 : 163-10-00275
Copyright © 2013 우리문화신문. All rights reserved. mail to pine9969@hanmail.net
UPDATE: 2025년 01월 04일 11시 41분
