[한국문화신문 = 이규봉 교수] 서양에서는 기원전 3500년 전부터 울림이 좋은 음 간격을 찾아서 조율을 했고, 옥타브 사이의 음들을 적당한 간격으로 나누어 다음 옥타브 위에 반복해 사용했다. 서양음악의 음계를 최초로 체계화 한 사람은 고대 그리스의 피타고라스이다. 피타고라스는 수학적 원칙을 기본으로 체계적인 조율을 했다. 중국에서는 삼분손익법(三分損益法)을 이용하여 음을 생성했다. 음을 생성하는 방법으로 피타고라스 방법이나 삼분손익법은 모두 인간이 인위적으로 만들었다고 보기보다는 자연의 법칙으로 소리가 발생하는 원리를 그대로 이용한 것이다. 이 소리의 원리에 정수비가 포함되어 있다.
2:3과 피타고라스 방법
앞서 설명했듯이 팽팽한 줄을 튕기면 배음들이 함께 나온다. 한 옥타브 내에서 보면 이 음들은 2:3과 3:4 등의 주파수 비로 화음을 이룬다. 피타고라스 조율은 주어진 줄의 길이를 2:3의 비율로 줄이거나 늘리는 방법으로 5도씩 음을 쌓는 방법이다. 이 방법을 구체적으로 살펴보면, 다음 두 가지 방법으로 음을 각각 구한 후 서로 비교하여 정수비가 작은 것을 택해 음계를 만든다.
올려쌓는 방법 기준 줄의 길이의 반을 3/2배 늘리고, 또 다시 3/2배 늘리는 과정을 반복하되 그 길이가 기준 줄의 길이의 두 배 이상 커지면 반으로 나눈다. |
내려쌓는 방법 기준 줄의 길이의 반을 3/2배 늘리고, 또 다시 3/2배 늘리는 과정을 반복하되 그 길이가 기준 줄의 길이의 두 배 이상 커지면 반으로 나눈다.
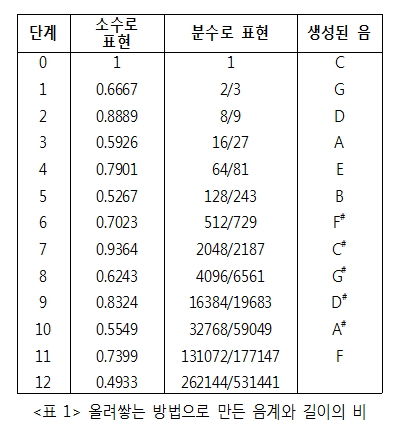
구체적으로 살펴보자. 올려쌓는 방법에서 음을 내는 처음 줄의 길이를 1이라고 하면 그 다음 줄의 길이는 2/3이다. 그 다음 줄의 길이는 4/9이나 이것은 1/2보다 작으므로(옥타브 위) 두 배하여 8/9이 된다. 세 번째 음은 두 번째 음의 2/3인 16/27이 된다. 네 번째 음은 32/81로 다시 1/2보다 작으므로 2를 곱하여 64/81가 된다. 이와 같은 과정에서 길이가 1/2보다 작게 되어 두 배 하는 과정이 포함된 곳은 ‘2, 4, 6, 7, 9, 11’번째로 모두 6곳이다.
기준 음을 C라고 하면 처음 생성된 음은 완전5도 높은 G음이 된다. 그 다음 과정에 한 옥타브 높은 D음이 생성되나 이를 두 배 했으므로 같은 옥타브 안의 D음이 생성된다. 이와 같은 과정을 계속 반복하면 <표 1>를 얻는다. 12번 째 생성된 음은 처음 음과 같지 않고 실제는 조금 높은 음이 되어 기본음과 12번 째 생성된 음의 간격은 한 옥타브를 약간 넘는다.
12번 째 생성된 음은 줄의 길이가 1/2보다 작으므로 첫 음의 옥타브보다 조금 높다. 두 배를 하여 옥타브 내로 조정한 524288/531441를 소인수 분해하면 219/312이다. 이 수의 역수는 약 1.0136으로 이 비를 ‘피타고라스 콤마’라 한다.
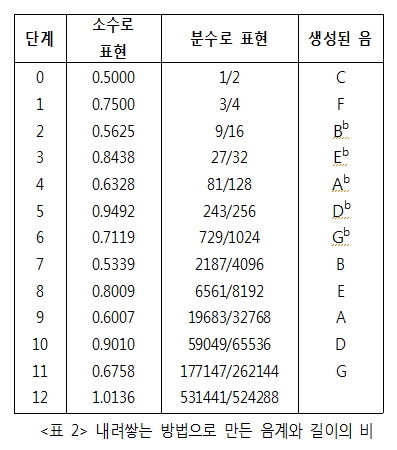
올려쌓는 방법과 내려쌓는 방법에서 같은 길이의 줄을 사용하면 내려쌓는 방법으로 생성된 음이 한 옥타브 아래가 된다. 따라서 올려쌓는 방법과 비교하기 위해서 내려쌓는 방법의 기본음을 내는 줄의 길이를 1/2이라고 하자. 그러면 그 다음 줄의 길이는 3/4이다. 그 다음은 9/8이나 이것은 1보다 크므로(옥타브 아래) 반으로 나누어 9/16가 된다. 세 번째 음은 두 번째 음의 3/2인 27/32이 된다. 네 번째 음은 81/64이 되나 1보다 크므로 반으로 나누어 81/128이 된다.
이와 같은 과정에서 길이가 1보다 크게 되어 반으로 나누는 과정이 포함된 곳은 올려쌓는 방법과 마찬가지로 ‘2, 4, 6, 7, 9, 11’번째 모두 6곳이다. 기본음을 C라고 하면 첫 번째 음은 완전5도 낮은 F음이 된다. 그 다음 과정에 한 옥타브 낮은 Bb음이 생성되나 반으로 나누었으므로 같은 옥타브 안의 Bb음이 생성된다. 이와 같은 과정을 또 다시 반복하면 <표 2>를 얻는다. 12번 째 생성된 음은 처음 음과 같지 않고 실제는 조금 낮은 음이 되어 올려쌓기와 마찬가지로 기본음과 12번 째 생성된 음의 음 간격은 한 옥타브를 약간 넘는다.
<표 2>에서 나온 길이의 비를 두 배하여 역수로 만들면 <표 1>의 길이 비가 된다. 이 두 표를 비교하면 같은 음정에서 올려쌓은 음정이 내려쌓은 음정보다 조금 더 높은 음이나 이웃한 음의 간격은 같음을 알 수 있다. 또한 이웃한 반음 사이의 간격은 일정하지 않고 따라서 온음 사이의 간격도 모두 같은 것은 아님을 알 수 있다.
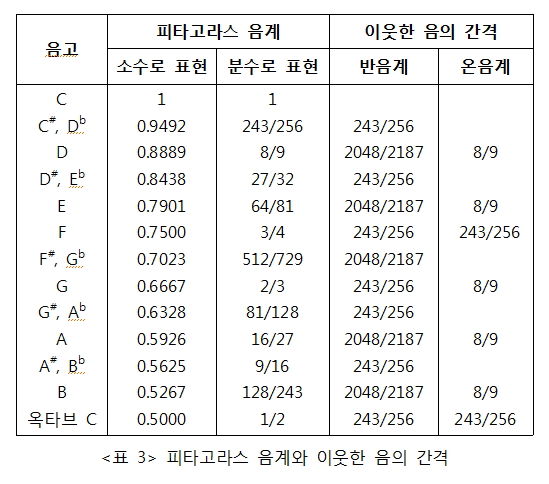
올려쌓은 음계와 내려쌓은 음계의 각 음의 비 중 작은 정수비를 택하여 나열한 피타고라스 음계는 <표 3>과 같다. 이 음계는 기본음과 올려쌓는 방법으로 만들어진 처음 6개 음 그리고 내려쌓는 방법으로 만들어진 처음 5개 음으로 이루어져 있다.
<표 3>에서 보듯이 피타고라스 음계는 온음의 비가 8/9로 동일하며 반음 사이도 모두 243/256로 같다. 그러나 반음의 비는 243/256과 2048/2187으로 모두 같은 것은 아니다. 피타고라스 음계를 따르면 기본음보다 한 음 높은 음은 줄의 길이가 기본음일 때 길이의 8/9일 때 나오며, 반음 높은 음은 기본음일 때 줄의 길이의 243/256일 때 나온다.
C보다 반음 높으면 C#이고 C#보다 반음 높으면 D이다. 그러나 C를 내는 줄의 길이를 1로 보았을 때
0.8889 = 8/9 < 243/256 x 243/256 = 0.9010
이므로 반음씩 두 번 올라온 음이 온음 높은 것보다 음이 낮다. 피타고라스 콤마는 반음씩 두 번 올라 온음이 되기 위해 부족함을 메우는 수로 사용된다. 곧
8/9 x 531441/524288 = 243/256 x 243/256
으로 반음정 올린 음(#)과 반음정 내린 음(b) 사이의 간격이 피타고라스 콤마이다.